Домашнее задание по теме "Обзор основных направлений ИИ"

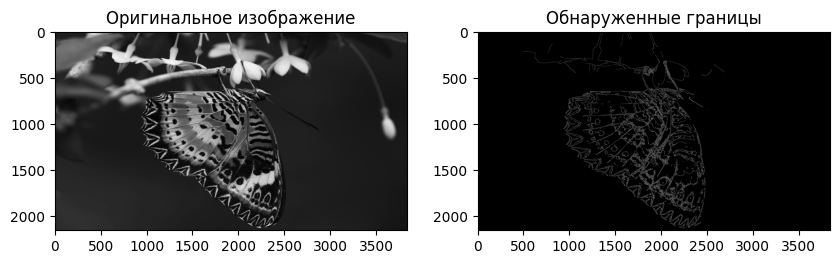
Канни Эдж Детектор (Canny Edge Detector) — это один из самых известных и широко используемых алгоритмов для обнаружения границ в изображениях.

Этапы работы Канни Эдж Детектора

1. Сглаживание изображения (Noise Reduction): Первым шагом является применение гауссового фильтра для снижения шумов в изображении. Это делает границы более четкими.

2. Градиентное преобразование (Gradient Computation): Вычисление градиентов изображения, чтобы определить направление и величину изменений интенсивности. Обычно используются операторы Собеля для этого этапа.

3. Ненаправленное подавление (Non-Maximum Suppression): В этом этапе выделяются только те пиксели, которые являются локальными максимумами вдоль направления градиента. Это помогает избавиться от менее выраженных границ.

4. Двойной порог (Double Thresholding): Установка двух пороговых значений для определения сильных и слабых границ. Пиксели, которые превышают высокий порог, считаются границами, а те, что между двумя порогами, будут проверены на связь с сильными границами.

5. Связывание границ (Edge Tracking by Hysteresis): Связывание слабых границ с сильными для окончательного определения границ. Слабые границы, которые соединяются с сильными, считаются границами.

Пример реализации Канни Эдж Детектора на Python

Вот пример кода на Python, который использует библиотеку OpenCV для реализации Канни Эдж Детектора:

import cv2
import numpy as np
import matplotlib.pyplot as plt

# Загрузка изображения
image = cv2.imread('/content/ED.jpg', cv2.IMREAD_GRAYSCALE)

# Применение гауссового фильтра для снижения шумов
blurred_image = cv2.GaussianBlur(image, (5, 5), 1.4)

# Применение Канни Эдж Детектора
edges = cv2.Canny(blurred_image, 50, 150)
# 50 и 150 - это  high threshold и low threshold —
# два пороговых значения, которые используются
# для определения сильных и слабых границ на изображении.

# Отображение результата
plt.figure(figsize=(10, 5))

plt.subplot(1, 2, 1)
plt.title('Оригинальное изображение')
plt.imshow(image, cmap='gray')

plt.subplot(1, 2, 2)
plt.title('Обнаруженные границы')
plt.imshow(edges, cmap='gray')

plt.show()

Результат:

Домашнее задание

Создайте текстовую ячейку в блокноте и напишите в ней свое понимание ответов на следующие вопросы:

1. Объясните этапы работы Канни Эдж Детектора. Почему каждый этап важен для общего алгоритма?

2. Как выбор значений для двойного порога (high и low threshold) влияет на результаты работы Канни Эдж Детектора?

   • Поэксперементируйте с примером кода и опишите свои наблюдения.

3. **Используйте Канни Эдж Детектор для различных изображений и сравните результаты. **

4. Используйте приведенный ниже код для визуализации градиентов в изображении. Подумайте: как можно использовать эти градиенты для других задач в компьютерном зрении?

5. Сохраните свой блокнот, расшарьте его и направьте ссылку на ваш блокнот на проверку преподавателю.

NB! Не забудьте загрузить в колаб изображения для тестирования (используйте фотографии из своих источников или интернета).

Замените в коде ссылки на изображения, использованные преподавателем, на ваши. Как это сделать - показано в лекции.

import cv2
import numpy as np
import matplotlib.pyplot as plt

# Загрузка изображения
image = cv2.imread('/content/ED.jpg', cv2.IMREAD_GRAYSCALE)

# Применение оператора Собеля для вычисления градиентов по осям X и Y
sobel_x = cv2.Sobel(image, cv2.CV_64F, 1, 0, ksize=5)  # Градиент по оси X
sobel_y = cv2.Sobel(image, cv2.CV_64F, 0, 1, ksize=5)  # Градиент по оси Y

# Вычисление величины градиента
gradient_magnitude = np.sqrt(sobel_x**2 + sobel_y**2)

# Нормализация градиентов для отображения
sobel_x = cv2.convertScaleAbs(sobel_x)
sobel_y = cv2.convertScaleAbs(sobel_y)
gradient_magnitude = cv2.convertScaleAbs(gradient_magnitude)

# Отображение результатов
plt.figure(figsize=(15, 5))

plt.subplot(1, 4, 1)
plt.title('Оригинальное изображение')
plt.imshow(image, cmap='gray')

plt.subplot(1, 4, 2)
plt.title('Градиент по оси X')
plt.imshow(sobel_x, cmap='gray')

plt.subplot(1, 4, 3)
plt.title('Градиент по оси Y')
plt.imshow(sobel_y, cmap='gray')

plt.subplot(1, 4, 4)
plt.title('Величина градиента')
plt.imshow(gradient_magnitude, cmap='gray')

plt.show()

Результат: